この図の真ん中の透明球が地球を表している。太陽(sun)からの光が届く範囲は、図の中の平面の上側であるのは明らかだろう。この平面が、"地球に対する太陽の位置ベクトルを法線ベクトルとする、地球中心を通る平面"だ。見てわかる通り、この平面に地軸(axis)が含まれる時、あらゆる地点において昼夜の長さが同じになる。図を見れば明らかなように、この平面内で地軸がどう動いても、この時点が春分の日であることに変わりはない。そして、このことと、このようにして得られる全ての平面にz軸に平行な直線が含まれることから、地軸のz軸方向の傾きは、無視して良いことがわかる。変な座標軸があるけど、ここでは無視して、後の説明に使うものなので。。

歳差運動による春分の日の変化

次に、地軸が変化することで春分の日がどう影響を受けるか見ていく。

f:id:babyron64:20180827235616p:plain

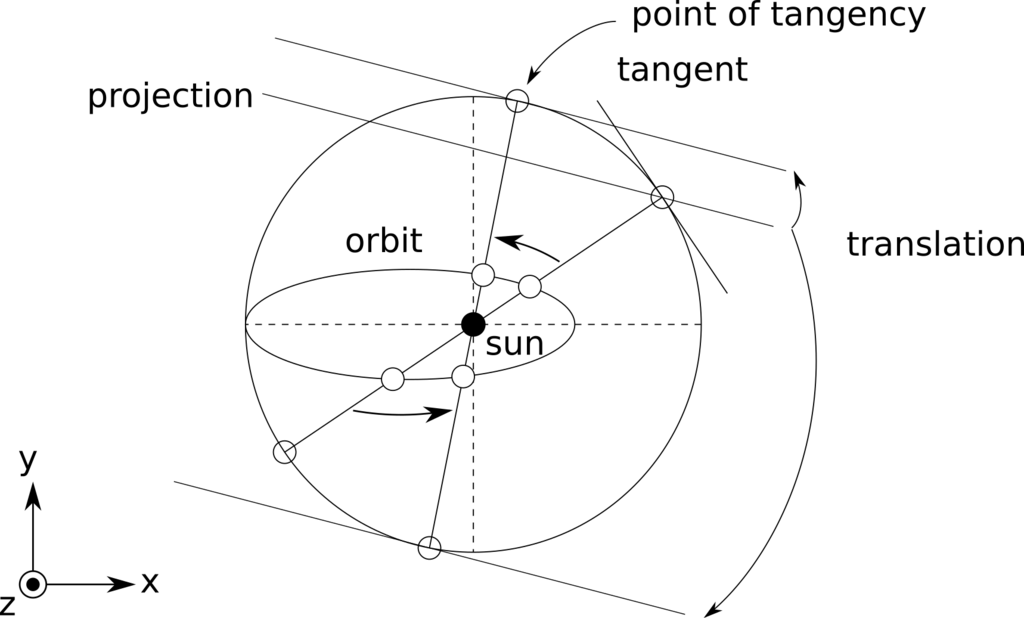
図中の白丸は地球、黒丸は太陽、楕円は地球軌道を表している。そして、外側の円（以降、外円という）は、太陽を中心として地球軌道に接するような円である。図には二つ地球が描いてあるが、上側の白丸が春分の日、下側が秋分の日を表している（後で説明）。太陽から春分の日の地球の位置へ伸ばした半直線が外円と交わる地点に、地球の太陽に対する位置ベクトルを法線ベクトルとする平面をとる（図中の垂直平面）。平面上には、交点（丸）、外円の接線(tangent)（実直線）、およびz軸に平行で交点を通る直線（点線）を書き込む。その平面を倒して水平にすると、先ほどの図が得られたとする。つまり、地軸の方向が図のようであったとする。（再掲する）

f:id:babyron64:20180828000356p:plain

ここから歳差運動で地軸がずれ、以下の図のようになったとする。

f:id:babyron64:20180828001937p:plain

このとき、この時点は春分の日ではなくなるのだが、では、春分の日はどこに変わったのだろうか。それをこれから見ていく。先ほどの言ったように、地軸のz軸成分は無視できるので、以降は地軸をxy平面に投影したもの(projection)を考えていく。

f:id:babyron64:20180828002638p:plain

xy平面は、地球の軌道を含む平面（黄道面）なので、地球の軌道上に地軸を書き込むことができる。

f:id:babyron64:20180828002833p:plain

春分の日の特徴は、

地球に対する太陽の位置ベクトルを法線ベクトルとする、地球中心を通る平面に、地軸が含まれる。

だったが、これは、

地軸の投影直線と太陽と地球を結ぶ直線が垂直である。

と言い換えることができる。また、円の性質として、接線と、中心と接点を結ぶ直線は直交するので、地軸の投影直線を平行移動(translation)させた直線と外円が接する場所(point of tangency)と、太陽を結ぶ直線と、地球軌道の交点に地球があるときに、春分の日になることがわかる。もう、言葉で説明しても訳がわからないと思うので、上の図を見て頑張って考えて。

このようにして、地軸の移動と春分の日の移動が関係しているのだ。

春分の日と秋分の日

上の図を見て、春分の日が二つあるじゃないかと思ったと思う。もちろんそんなことはなく、実は、片方は秋分の日を表しているのだ。先ほど、春分の日の特徴として、昼の長さと夜の長さが同じことを使ったが、これは当然秋分の日にも当てはまる。春分点のwikipediaの定義は、

春分点（しゅんぶんてん、英: vernal equinox）とは、黄道と天の赤道との2つの交点（分点）のうち、黄道が南から北へ交わる方の点（昇交点）のこと。

となっているが、僕らは"南から北へ"という条件を使っていないのだ。これが"北から南へ"となるのが秋分の日という訳だ。

この定義を使うために、まずは、この記事での南北の定義を与える。

右手系における、地球の自転の回転ベクトルの方向。南はその反対方向。

面倒な定義をしたが、ようするに、地球の自転が反時計回りに見える方を北とするというだけのことだ。これは実生活で何気なく用いている"北"という言葉の語感と一致する。北極がある方が北なのだ（いや、北だから北極なんだろう？）。

そして、地球軌道面の北側より南側の方が地軸と太陽が離れているとき太陽は北側にあるし、逆ならば太陽は南側にある。つまり、上の図でどちらが春分でどちらが秋分なのかは、地軸の傾き方や軌道面の方向に依存するので、定めることができない。

これで終わるのは物足りないので、よくみる下のような図について説明を加えて終わりにしよう。

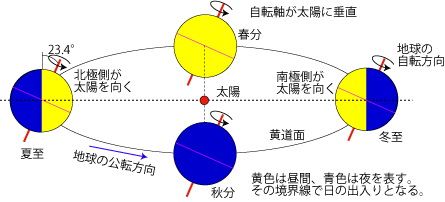
これは、国立天文台から借りたものだ。この図では地軸の傾きや軌道面の向き（自転方向）、公転方向が明示してあるので、春分の日と秋分の日の見分けがつく。図で見て変わるように、冬至の日には太陽は最も南にあり、春分を経て夏至の日になると最も北にある。そして、秋分を経て冬至に戻る。そして、春分の日こそ、太陽が"南から北"に移る日だ。

2018-08-23

javascriptを使ったHTML要素の位置取得

html javascript web

javascriptから取得できるHTML要素の位置は様々な種類があるので、後から参照できるようにまとめておく。jqueryなどのライブラリを使う方法については省略。ネイティブ環境で使えるもののみ扱う。各見出しはMDN web docsへのリンクになっているので、詳細はそちらを参照。

HTML要素の位置取得
mouseイベント、touchイベントの位置取得
viewport上の位置への変換
参考
- page、screen、viewportとかの関係
  - スマホの場合 (iphone上のsafariとchromeで確認)
  - パソコンの場合 (mac上のsafariで確認)
- 外部ページ

HTML要素の位置取得

style.xxx

基本情報

cssのプロパティを取得、設定する。

getBoundingClientRect()

基本情報

相対要素	margin	border	padding
viewport	x	o	o

viewport相対なので、scrollによって変化する。

取得できる値

大体はgetClientRects()と同じだが、こちらで取得すると要素のボーダーを含む全体についての値が得られる。

top
left
bottom
left
x
y
width
height

getClientRects()

基本情報

相対要素	margin	border	padding
viewport	x	o	o

viewport相対なので、scrollによって変化する。

取得できる値

大体はgetBoundingClientRect()と同じだが、こちらで取得すると一行ずつの値がリストで得られる。一行ずつというのは、インライン要素が途中で折り返して複数行に渡って表示される場合、各行についての値を取得できるということ。ブロック要素の場合は、リストの要素は一つだけ。この要素は、getBoundingClientRect()で得られるものと同じ。

[
- top -left
- bottom
- left
- x
- y
- width
- height
]

getClientRects()についての参考

<div>
 <strong>span's rect</strong>
 <p>
  <span>Paragraph that spans multiple lines</span>
 </p>
</div>

上の画像において、span's rectにおいて赤色で示されているのが、spanの各行に関するgetClientRects()の戻り値。

[read-only] offsetTop

[read-only] offsetLeft

相対要素	margin	border	padding
offsetParent	x	o	o

取得できる値

offsetTopとoffsetLeftは、offsetParentに対する一行目の相対位置。すなわち、getClientRects()が返すリストの初めの要素をoffsetParentが基準となるように変換しても得られる。

offsetTop

offsetTop

offsetLeft

offsetLeft

[read-only] offsetWidth

[read-only] offsetHeight

相対要素	margin	border	padding
offsetParent	x	o	o

取得できる値

offsetWidth

offsetWidth

offsetHeight

offsetHeight

offsetxxxについての参考

[read-only] offsetParent

positionがrelative、absolute、fixedのいずれかである要素のうち直近の先祖。

取得できる値

<div>
  <span>Short span. </span>
  <span>Long span that wraps within this div.</span>
</div>

この画像の中で赤色で示されているものが、二つ目のspanのoffsetxxxの値。top、left、width、heightに二つ目のspan要素のoffsetxxxで得られる値を設定している。

mouseイベント、touchイベントの位置取得

mouseイベントやtouchイベントでは、clickまたはtouchした場所を取得できる。その値と実際の場所の関係を書いておく。

f:id:babyron64:20180823194945p:plain

上の図では、pointで示される場所にclickまたはtouchしたと想定している。

viewport上の位置への変換

何らかの基準に対する相対位置が得られたときに、それをviewport上への位置に変換する方法を書いておく。先ほど示したように、pageとviewportの関係は、window.pageX/YOffsetで得られる。これはすなわちbodyとviewportの関係なので、viewportに対する相対位置にwindow.pageX/YOffsetを加えることで、body上での位置が得られる。

具体的には、

var client_rec = document.getElementById(...).getBoundingClientRect();
var element_x = window.pageXOffset + client_rec.x;
var element_x = window.pageYOffset + client_rec.y;

とすることで、elementの座標element_xとelement_yが得られる。

参考

page、screen、viewportとかの関係

スマホの場合 (iphone上のsafariとchromeで確認)

f:id:babyron64:20180823200436p:plain

基本的には上の図のようになるが、viewportが画面に収まるようにブラウザが自動的に拡大・縮小することがある。

パソコンの場合 (mac上のsafariで確認)

f:id:babyron64:20180823200559p:plain

外部ページ

もう逃げない。HTMLのviewportをちゃんと理解する

2018-08-23

ARMのレジスタ達

arm stm32

x86_64のレジスタ名なら知っているけど、armのレジスタ名はまた違うからややこしい。armのリファレンスを読むときに混乱しないように、ここでまとめておく。

レジスタ名	役割
r0~r12	汎用レジスタ
r13 (sp)	スタックポインタ
r14 (lp)	リンクレジスタまたは汎用レジスタ
r15 (pc)	プログラムカウンタ

r14 (lp)には復帰アドレスを格納する。ただし、スタックに復帰アドレスを積む場合には、汎用レジスタとしてつかえる。

r15 (pc)にはmov命令でアドレスがロードできる。サブルーチンから戻るには、 MOV pc,lr とすれば良い。

2018-08-18

Homogeneous(同次)座標系を使ったClipping

OpenGL 座標 graphics

OpenGLライブラリの中には、glClipPlane(https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glClipPlane.xml)という関数がある。この関数は平面を表すベクトル(というより、数の組)を受け取り、受け取った平面でクリッピングを行う。クリッピングの方法として、

If the dot product of ... a vertex with the stored plane equation components is positive or zero, the vertex is in with respect to that clipping plane. Otherwise, it is out.

と書かれているが、これで本当にクリッピングができるのか考えてみた。

前提

plane equation components

三次元空間内の二次元平面は、 $Ax+By+Cz+D=0$ と表せる。すなわち、(A, B, C, D)の4つの数字の組で平面を指定できる。これがplane equation componentsだ(と思う)。そして、両辺に0でない数をかけても表す平面は変わらない。たとえば、 $-Ax-By-Cz-D=0$ も $Ax+By+Cz+D=0$ と同じ平面を表している。

homogeneous座標系

cartesian座標系で(x, y, z)と表される点は、homogeneous座標系においては0でない任意数wを新たに導入して(wx, wy, wz, w)と表される。とくに、w=1のとき（普通はそうする）は(x, y, z, 1)となる。wは遠近法を考えるときに使えたりするのだけれど、省略。homogeneous座標系についての詳細はhttps://en.wikipedia.org/wiki/Homogeneous_coordinatesとかで読んでね。以降の説明では、homogeneous座標系の点(x, y, z, 1)とcartesian座標系の点(x, y, z)を同一視する。

考えてみる

the dot product of a vertex with the stored plane equation componentsは、vertexの座標を $(v _ x, v _ y, v _ z, 1)$ 、平面の方程式を $Ax+By+Cz+D=0$ とすると、 $dot = Av _ x+ Bv _ y+Cv _ z+D$ となる。ここで、dotはdot product（ie. 内積）を表している。以降、vertexと点を同一視する。

Dが0でないとき

plane equation components (A, B, C, D)で構成される平面 $Ax+By+Cz+D=0$ （以降、 $\alpha$ とする）上の、あるvertexの座標が $(v _ x, v _ y, v _ z, 1)$ だったとする。すると、

${ \begin{align} Av _ x+Bv _ y+Cv _z+D &= 0 \\\ Av _ x+Bv _ y+Cv _z &= -D \end{align} }$

より、cartesian座標が $(sv _ x, sv _ y, sv _ z)$ であるようなvertexとの内積は、

${ \begin{align} dot &= Asv _ x+Bsv _ y+Csv _ z+D \\\ &= -sD+D \\\ &= (1-s)D \end{align} }$

となる。これは、平面 $\alpha$ 上の任意のvertexについて成り立つので、平面 $\alpha$ に平行な各平面上のvertexたちの内積は一定であることがわかる。さらに、三次元空間内の任意の点は平面 $\alpha$ に平行な平面の内どれか一つの上にあるので、これまでの議論で空間内のすべてのvertexについての内積を考えられる。下図ではこのことを模式的に表している。
f:id:babyron64:20180818023849p:plain

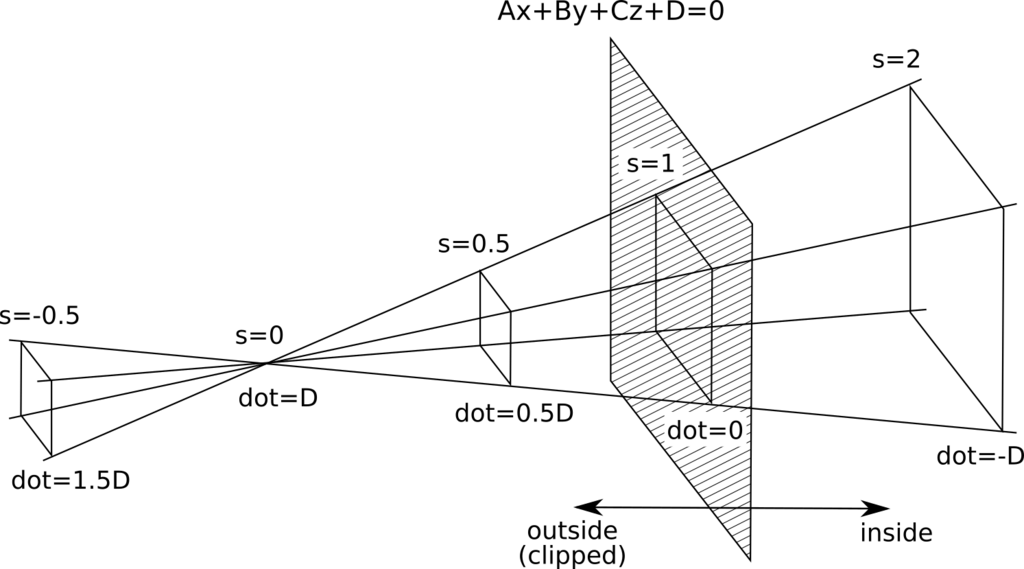
dotが正であるところがクリッピングされるのだったから、Dが正だとすると、この場合は平面に対して左側がクリッピングされることになる。

一方、plane equation components (-A, -B, -C, -D)で構成される平面 $-Ax-By-Cz-D=0$ もまた平面 $\alpha$ である。この場合についても先ほどと同じように考えてみる。平面 $\alpha$ 上のあるvertexの座標が $(v _ x, v _ y, v _ z, 1)$ だったとする。すると、

${ \begin{align} -Av _ x+Bv _ y-Cv _z-D &= 0 \\\ -Av _ x-Bv _ y-Cv _z &= D \end{align} }$

より、cartesian座標が $(sv _ x, sv _ y, sv _ z)$ であるようなvertexとの内積は、

${ \begin{align} dot &= -Asv _ x-Bsv _ y-Csv _ z-D \\\ &= sD-D \\\ &= (s-1)D \end{align} }$

となり、先ほどの場合のdotの値(1-s)Dとは符号が反転している。この場合の模式図は、
f:id:babyron64:20180818025104p:plain

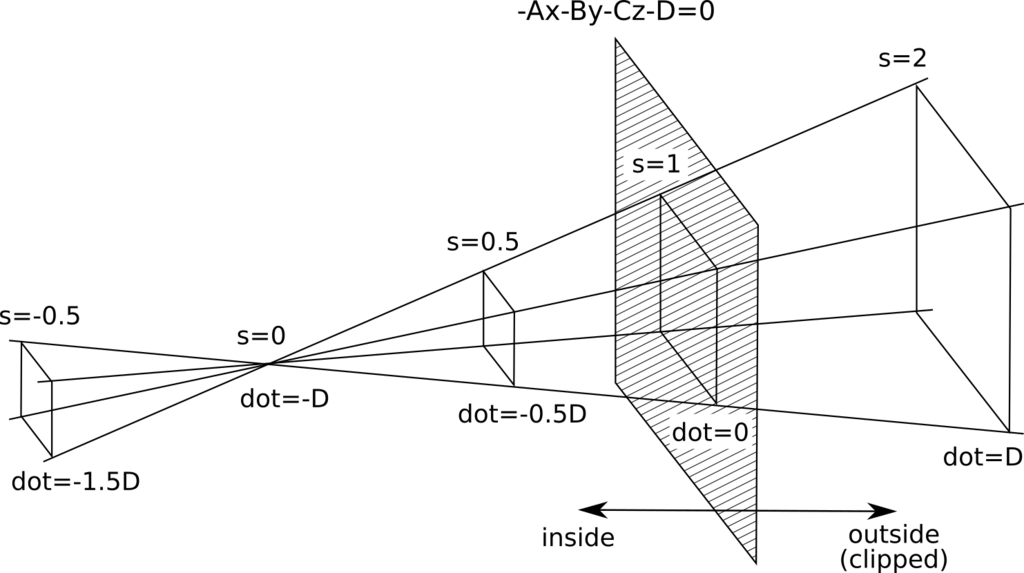
となるので、Dが正だとすると、平面に対して右側がクリッピングされることになる。先ほどは左側がクリッピングされていたので、クリッピングの範囲が入れ替わっている。

Dが0でないときのまとめ

Dが0でないときには、Dの符号によってクリッピングされる範囲を瞬時に判断することができる。plane equation componentsが(A, B, C, D)であるとき、D>0ならば平面によって分けられた二つの空間のうち、原点を含む方がクリッピングされ、D<0ならば、原点を含まない方がクリッピングされる。

このような仕組みで、単純に内積を取るだけでクリッピングができる。だが、D=0の場合には上の議論は破綻してしまう。模式図を見ても、D=0の時には全ての平面が一つになってしまうので、空間内の全てのvertexの内積について言及していないことが明らかにわかる。そこで、D=0のときは別に考えてみる。

Dが0のとき

plane equation componentsが(A, B, C, 0)であり、それが構成する平面を $\alpha$ とするとき、ベクトルv(A, B, C)と平面 $\alpha$ は直行する。軽く説明しておくと、平面 $\alpha$ 上の任意の点P(s, t, u)について、平面 $\alpha$ 上にあるために $As+Bt+Cu=0$ だが、これはまさしくベクトルvとPの位置ベクトルが直交することを意味している。そして、Pは任意点なので、ベクトルvと平面 $\alpha$ は直行していることがわかるといった具合。まあ、直交していることはのちの議論では使わず、ただ単に、位置ベクトル(A, B, C)が表す点がが平面に含まれることはないということが言いたかっただけ。

plane equation componentsが(A, B, C, 0)であり、それが構成する平面を $\alpha$ とする。座標が $(v _ x, v _ y, v _ z, 1)$ のvertexの内積 $dot = Asv _ x+Bsv _ y+Csv _ z$ は、ベクトル(A, B, C)とベクトル $(v _ x, v _ y, v _ z)$ の内積に等しい。これより下図のように、ベクトル $(v _ x, v _ y, v _ z)$ が平面 $\alpha$ に対してベクトル(A, B, C)と同じ方向にあるときはdotが正、逆方向にあるときはdotが負になる。
f:id:babyron64:20180818031146p:plain
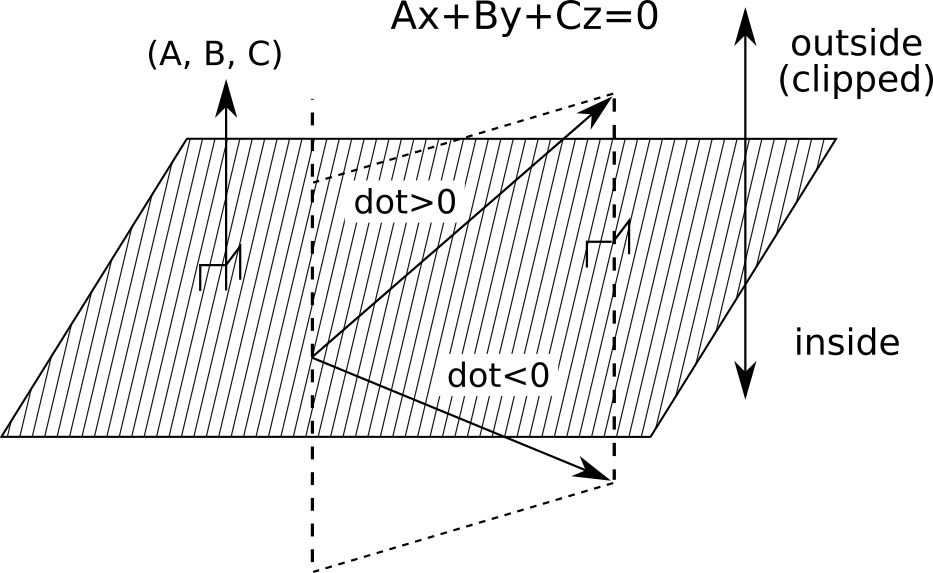
よってこの場合、平面 $\alpha$ の上側がクリッピングされる。

一方、plane equation componentsが(-A, -B, -C, 0)であるときも、それが構成する平面は $\alpha$ と同じである。先ほどと同じように考えると、ベクトル $(v _ x, v _ y, v _ z)$ が平面 $\alpha$ に対してベクトル(-A, -B, -C)と同じ方向にあるときはdotが正、逆方向にあるときはdotが負になる。
f:id:babyron64:20180818031350p:plain
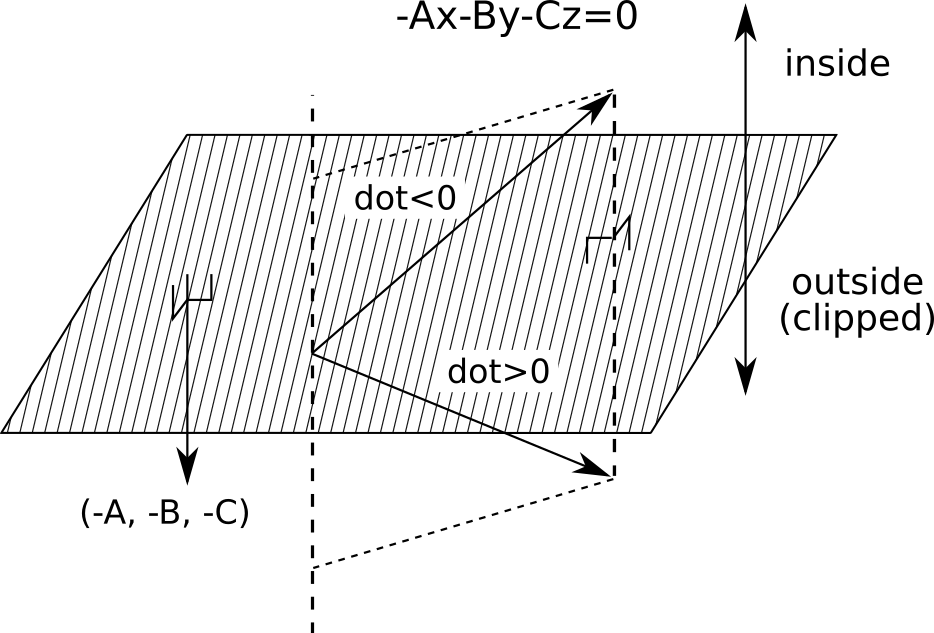
よってこの場合には、平面 $\alpha$ の下側がクリッピングされる。

Dが0のときのまとめ

D=0のとき、plane equation componentsが(A, B, C, 0)ならば、平面によって分けられた二つの空間のうち、位置ベクトル(A, B, C)によって表される点を含む方が（ie. ベクトル(A, B, C)がさす方の空間が）クリッピングされる。位置ベクトル(A, B, C)によって表される点は先ほど言ったように、平面に含まれることはないので、クリッピングする空間は必ず定まる。

まとめ

homogeneous座標系は平行移動が行列の掛け算で表せるなどの利点がよく引き合いに出されるが、このようにクリッピングを行ううえでも便利だ。また、記事の中でも少し触れたけど、遠近法に関する計算も楽にできる。例えば、vertexを遠近法を考慮して平面に投影させることを考える。まず、視点(カメラの位置)が原点、投影面がz=1となるようにcartesian座標をとる。各vertexのhomogeneous座標をcartesian座標から、(x, y, z) -> (x, y, z, z)となるように定める。そののち、各vertexのhomogeneous座標を第四成分が1となるように規格化（各成分を第四成分で割る）する。規格化後の座標が(x', y', 1, 1)なら、投影後の座標は(x', y')だ。このように、遠近法に関する計算を楽に行える。だから、homogeneous座標系はグラフィックス分野で多用されるらしい（本当はこの分野に来てまだ３日なので何もわかってない）。

2018-08-05

デバッグ情報を探る〜.cfi_xx命令の動作〜

dwarf debug linux gdb

次のようなc言語プログラムを例にとって考えていく。

// test.c

int hoge(int x)
{
    return x+1;
}

int main()
{
    int a = 1;
    return hoge(a);
}

gcc -O0 -S test.cを実行してコンパイルすると、

; test.s

_hoge:
    .cfi_startproc

    pushq    %rbp
    .cfi_def_cfa_offset 16
    .cfi_offset %rbp, -16

    movq %rsp, %rbp
    .cfi_def_cfa_register %rbp

    movl %edi, -4(%rbp)
    movl -4(%rbp), %edi
    addl $1, %edi
    movl %edi, %eax
    popq %rbp
    retq
    .cfi_endproc

_main:
    .cfi_startproc

    pushq    %rbp
    .cfi_def_cfa_offset 16
    .cfi_offset %rbp, -16

    movq %rsp, %rbp
    .cfi_def_cfa_register %rbp

    subq $16, %rsp
    movl $0, -4(%rbp)
    movl $1, -8(%rbp)
    movl $1, -12(%rbp)
    movl -8(%rbp), %eax
    addl -12(%rbp), %eax
    movl %eax, %edi
    callq    _hoge
    addq $16, %rsp
    popq %rbp
    retq
    .cfi_endproc

このようなアセンブリが生成される。

.cfi_startproc擬似命令では、CFI (Call Frame Infomation)が新たに追加され、CFA (Canonical Frame Address)計算用のレジスタがrspに、オフセットが0に初期化される。続くpushqではrbpをスタックに退避させている。そして、.cfi_def_cfa_offsetでCFAのオフセットを16にしている。このときのスタックには、

f:id:babyron64:20180805012254p:plain

のようにデータが格納されていく。

.cfi_offset %rbp, -16では、rbpレジスタの値をCFA-16のアドレスに退避させたことを表している。実際、rbpレジスタの値はスタックの先頭にあるので、(rsp-16)+16 = rspはrbpレジスタの値が格納されているアドレスを表す。僕はここで少しハマったのだが、rbpの値が格納されているアドレスはrsp-8ではない。スタックは成長するにつれてアドレスが減るからだ。(下図参照)

f:id:babyron64:20180805012242p:plain

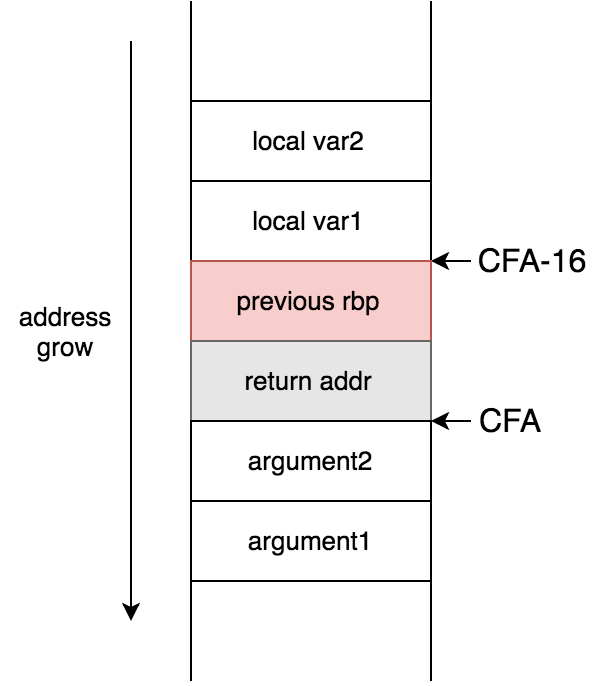
実際例えば、

mv (%rsp-16+16) %rx

とすることで、rxレジスタにrbpの元の値を格納できる。

その後、CFAのレジスタを.cfi_def_cfa_register %rbpとすることで、このフレームのCFAを固定している。rspを参照レジスタにすると、スタック操作をするたびにCFAが変わってしまう。

最後に、.cfi_endprocで前のフレームのCFAを復元している。これらの命令によって生成された情報は、デフォルトでは.eh_frameセクションに保存される。

2018-08-01

レジスタ制御用ワンライナー達

c ビットマイコン

変数regにマップされたレジスタを、ビット演算子で制御する。

マスクを用意

msk = 1U << x;

AND (&)

xビットを取ってくる

bit = (reg & msk) >> x;

xビットをクリア

reg &= ~msk;

xビット以外をクリア

reg &= msk;

xビットによる条件分岐 (1bit)

if (reg & msk)    // ビットが立っていれば、、、
    ;
else
    ;

xビットによる条件分岐 (マルチbit)

if ((reg & msk) == msk)    // ビットが立っていれば、、、
    ;
else
    ;

OR (|)

xビットを立てる

reg |= msk;

XOR (^)

xビットをトグル

reg ^= msk;

番外編

下位xビットをとってくる

reg & (msk - 1U)

マクロ内で変数を安全に使う方法

#define HOGE() do { \
    int new_var; \
    ... \
    } while(0);

2018-08-01

STM32F3探訪〜GPIOx_ODR vs GPIOx_BSRR 〜

stm32 マイコン

STM32F3のGPIOピンのoutput用レジスタには、GPIOx_ODRというものと、GPIOx_BSRRという二種類ある。その違いを調べたので、書き留めておく。

ODRとBSRRは共に書き込み可能なレジスタであり、GPIOのoutput値を決めるのに使える。BSRRはリファレンスに、

Bits 31:16 BRy: Port x reset bit y (y = 0..15)
These bits are write-only. A read to these bits returns the value 0x0000.
0: No action on the corresponding ODRx bit
1: Resets the corresponding ODRx bit

Note: If both BSx and BRx are set, BSx has priority.
Bits 15:0 BSy: Port x set bit y (y= 0..15)
These bits are write-only. A read to these bits returns the value 0x0000.
0: No action on the corresponding ODRxODR
1: Sets the corresponding ODRx bit

と書いてあるように、ODRを設定するためのレジスタである。では、ODRだけでいいじゃないかと思うかもしれないが、次のような場合の為に、BSRRが必要だ。

例

Port xのbit yピンを1にしたいときを考える。

ODRだけ

uint32_t odr = GPIOx->ODR;  # part 1
odr |= 1UL << y;            # part 2
GPIOx->ODR = odr;           # part 3

といった操作を行うことになる。しかし、part 1のあとに割り込みが入り、割り込みルーチンの中でODRが変更されたときを考えてほしい。part 3で書き戻したときに、その変更をなかったことにしてしまう。

ODRとBSRR

uint32_t bsrr = 1UL << y;   # part 1
GPIOx->BSRR = bsrr;         # part 2

という操作で実現できる。BSRRに0を書き込んでも何も起こらないからこのようにできる。この場合、part 1の後に割り込みが入っても、ODRのコピーをしていないので問題ない。また、命令数が単純に少なくなっているので実行が早くなる。

BSRRのこのような性質を指して、レファレンスではatomicという語を使っている。ただ、何の前置きもなしにatomicと言われても何のことかわからないので、例解してみた。

追記

ODRだけの時のコードは、

GPIOx->ODR |= 1UL << y;

と一行で書ける。しかし、この場合も生成されるバイナリ(ここでは擬似的なアセンブリで示す)は、

mv GPIOx->ODR, %r0
or 1UL << y, %r0
mv %r0, GPIO->ODR

といった感じになるので、一命令ではない。