Homogeneous(同次)座標系を使ったClipping

OpenGLライブラリの中には、glClipPlane(https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glClipPlane.xml)という関数がある。この関数は平面を表すベクトル(というより、数の組)を受け取り、受け取った平面でクリッピングを行う。クリッピングの方法として、

If the dot product of ... a vertex with the stored plane equation components is positive or zero, the vertex is in with respect to that clipping plane. Otherwise, it is out.

と書かれているが、これで本当にクリッピングができるのか考えてみた。

前提

plane equation components

三次元空間内の二次元平面は、 $Ax+By+Cz+D=0$ と表せる。すなわち、(A, B, C, D)の4つの数字の組で平面を指定できる。これがplane equation componentsだ(と思う)。そして、両辺に0でない数をかけても表す平面は変わらない。たとえば、 $-Ax-By-Cz-D=0$ も $Ax+By+Cz+D=0$ と同じ平面を表している。

homogeneous座標系

cartesian座標系で(x, y, z)と表される点は、homogeneous座標系においては0でない任意数wを新たに導入して(wx, wy, wz, w)と表される。とくに、w=1のとき（普通はそうする）は(x, y, z, 1)となる。wは遠近法を考えるときに使えたりするのだけれど、省略。homogeneous座標系についての詳細はhttps://en.wikipedia.org/wiki/Homogeneous_coordinatesとかで読んでね。以降の説明では、homogeneous座標系の点(x, y, z, 1)とcartesian座標系の点(x, y, z)を同一視する。

考えてみる

the dot product of a vertex with the stored plane equation componentsは、vertexの座標を $(v _ x, v _ y, v _ z, 1)$ 、平面の方程式を $Ax+By+Cz+D=0$ とすると、 $dot = Av _ x+ Bv _ y+Cv _ z+D$ となる。ここで、dotはdot product（ie. 内積）を表している。以降、vertexと点を同一視する。

Dが0でないとき

plane equation components (A, B, C, D)で構成される平面 $Ax+By+Cz+D=0$ （以降、 $\alpha$ とする）上の、あるvertexの座標が $(v _ x, v _ y, v _ z, 1)$ だったとする。すると、

${ \begin{align} Av _ x+Bv _ y+Cv _z+D &= 0 \\\ Av _ x+Bv _ y+Cv _z &= -D \end{align} }$

より、cartesian座標が $(sv _ x, sv _ y, sv _ z)$ であるようなvertexとの内積は、

${ \begin{align} dot &= Asv _ x+Bsv _ y+Csv _ z+D \\\ &= -sD+D \\\ &= (1-s)D \end{align} }$

となる。これは、平面 $\alpha$ 上の任意のvertexについて成り立つので、平面 $\alpha$ に平行な各平面上のvertexたちの内積は一定であることがわかる。さらに、三次元空間内の任意の点は平面 $\alpha$ に平行な平面の内どれか一つの上にあるので、これまでの議論で空間内のすべてのvertexについての内積を考えられる。下図ではこのことを模式的に表している。
f:id:babyron64:20180818023849p:plain

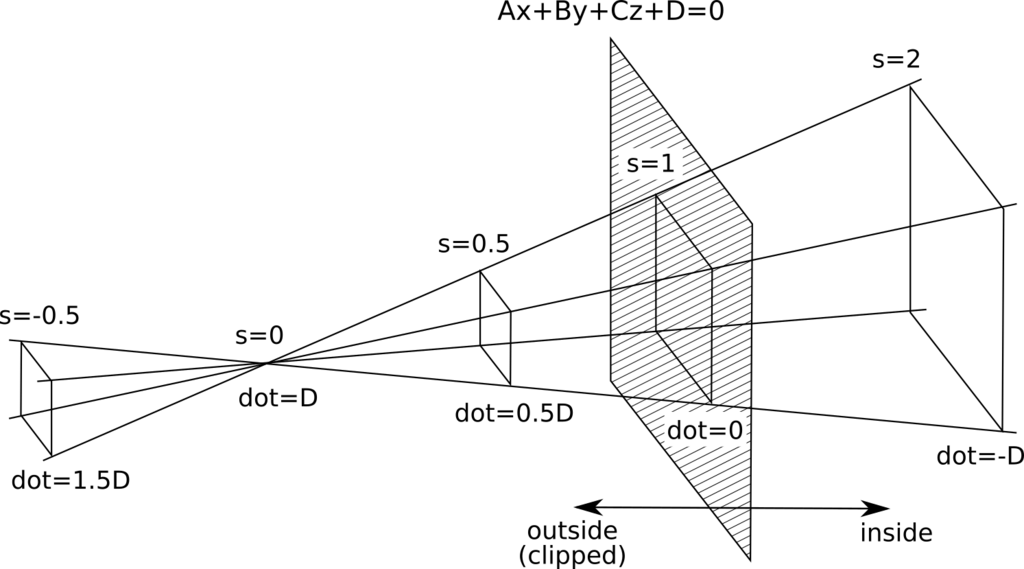
dotが正であるところがクリッピングされるのだったから、Dが正だとすると、この場合は平面に対して左側がクリッピングされることになる。

一方、plane equation components (-A, -B, -C, -D)で構成される平面 $-Ax-By-Cz-D=0$ もまた平面 $\alpha$ である。この場合についても先ほどと同じように考えてみる。平面 $\alpha$ 上のあるvertexの座標が $(v _ x, v _ y, v _ z, 1)$ だったとする。すると、

${ \begin{align} -Av _ x+Bv _ y-Cv _z-D &= 0 \\\ -Av _ x-Bv _ y-Cv _z &= D \end{align} }$

より、cartesian座標が $(sv _ x, sv _ y, sv _ z)$ であるようなvertexとの内積は、

${ \begin{align} dot &= -Asv _ x-Bsv _ y-Csv _ z-D \\\ &= sD-D \\\ &= (s-1)D \end{align} }$

となり、先ほどの場合のdotの値(1-s)Dとは符号が反転している。この場合の模式図は、
f:id:babyron64:20180818025104p:plain

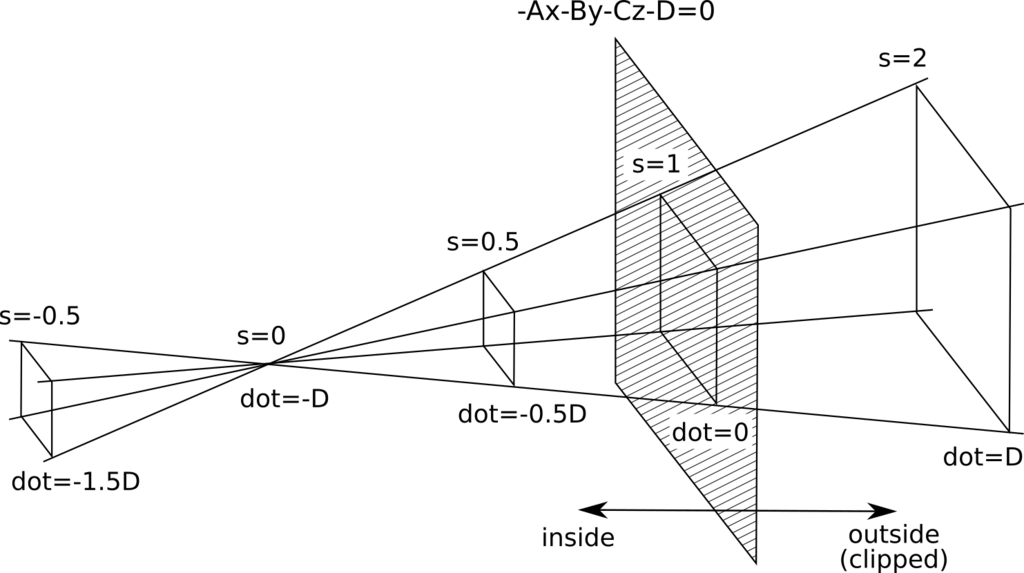
となるので、Dが正だとすると、平面に対して右側がクリッピングされることになる。先ほどは左側がクリッピングされていたので、クリッピングの範囲が入れ替わっている。

Dが0でないときのまとめ

Dが0でないときには、Dの符号によってクリッピングされる範囲を瞬時に判断することができる。plane equation componentsが(A, B, C, D)であるとき、D>0ならば平面によって分けられた二つの空間のうち、原点を含む方がクリッピングされ、D<0ならば、原点を含まない方がクリッピングされる。

このような仕組みで、単純に内積を取るだけでクリッピングができる。だが、D=0の場合には上の議論は破綻してしまう。模式図を見ても、D=0の時には全ての平面が一つになってしまうので、空間内の全てのvertexの内積について言及していないことが明らかにわかる。そこで、D=0のときは別に考えてみる。

Dが0のとき

plane equation componentsが(A, B, C, 0)であり、それが構成する平面を $\alpha$ とするとき、ベクトルv(A, B, C)と平面 $\alpha$ は直行する。軽く説明しておくと、平面 $\alpha$ 上の任意の点P(s, t, u)について、平面 $\alpha$ 上にあるために $As+Bt+Cu=0$ だが、これはまさしくベクトルvとPの位置ベクトルが直交することを意味している。そして、Pは任意点なので、ベクトルvと平面 $\alpha$ は直行していることがわかるといった具合。まあ、直交していることはのちの議論では使わず、ただ単に、位置ベクトル(A, B, C)が表す点がが平面に含まれることはないということが言いたかっただけ。

plane equation componentsが(A, B, C, 0)であり、それが構成する平面を $\alpha$ とする。座標が $(v _ x, v _ y, v _ z, 1)$ のvertexの内積 $dot = Asv _ x+Bsv _ y+Csv _ z$ は、ベクトル(A, B, C)とベクトル $(v _ x, v _ y, v _ z)$ の内積に等しい。これより下図のように、ベクトル $(v _ x, v _ y, v _ z)$ が平面 $\alpha$ に対してベクトル(A, B, C)と同じ方向にあるときはdotが正、逆方向にあるときはdotが負になる。
f:id:babyron64:20180818031146p:plain
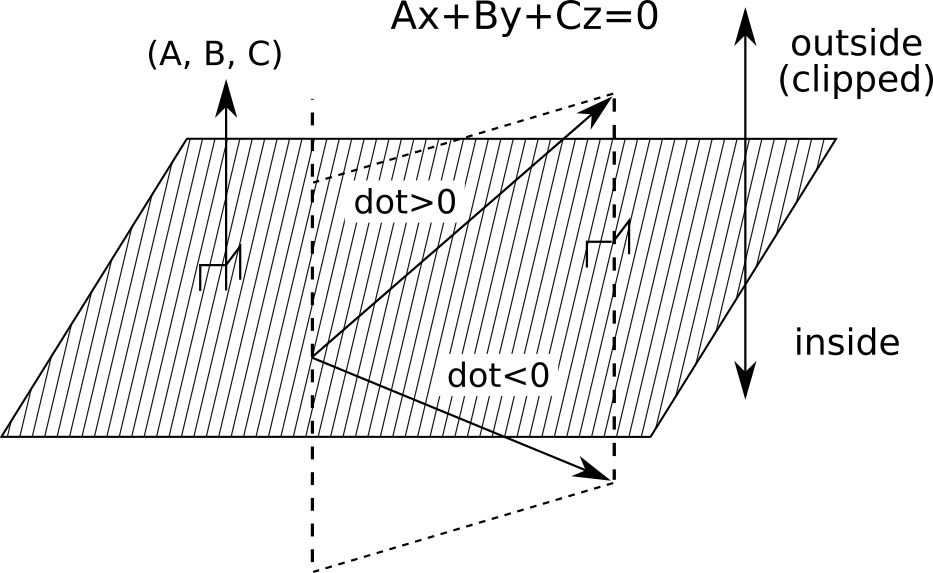
よってこの場合、平面 $\alpha$ の上側がクリッピングされる。

一方、plane equation componentsが(-A, -B, -C, 0)であるときも、それが構成する平面は $\alpha$ と同じである。先ほどと同じように考えると、ベクトル $(v _ x, v _ y, v _ z)$ が平面 $\alpha$ に対してベクトル(-A, -B, -C)と同じ方向にあるときはdotが正、逆方向にあるときはdotが負になる。
f:id:babyron64:20180818031350p:plain
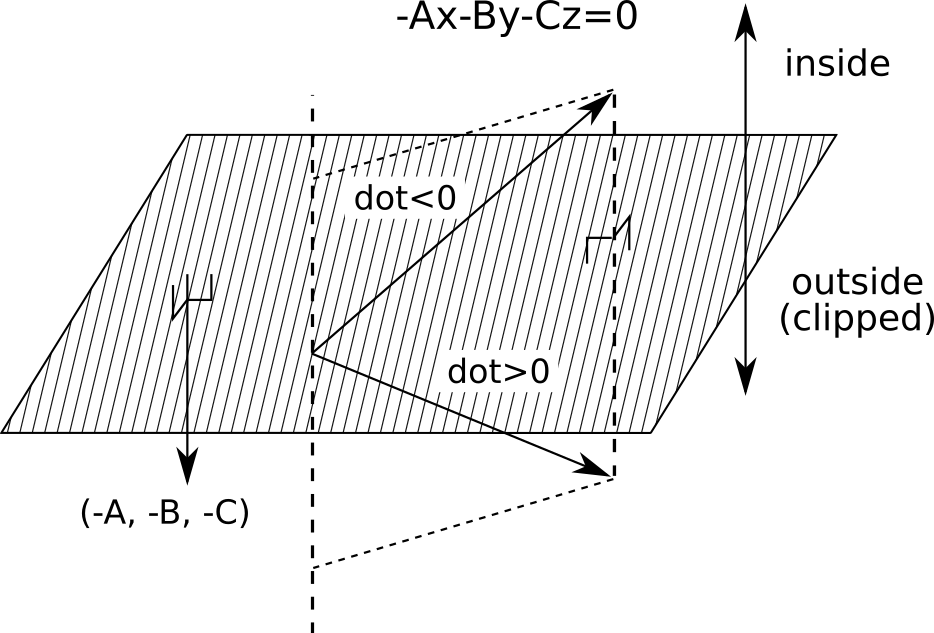
よってこの場合には、平面 $\alpha$ の下側がクリッピングされる。

Dが0のときのまとめ

D=0のとき、plane equation componentsが(A, B, C, 0)ならば、平面によって分けられた二つの空間のうち、位置ベクトル(A, B, C)によって表される点を含む方が（ie. ベクトル(A, B, C)がさす方の空間が）クリッピングされる。位置ベクトル(A, B, C)によって表される点は先ほど言ったように、平面に含まれることはないので、クリッピングする空間は必ず定まる。

まとめ

homogeneous座標系は平行移動が行列の掛け算で表せるなどの利点がよく引き合いに出されるが、このようにクリッピングを行ううえでも便利だ。また、記事の中でも少し触れたけど、遠近法に関する計算も楽にできる。例えば、vertexを遠近法を考慮して平面に投影させることを考える。まず、視点(カメラの位置)が原点、投影面がz=1となるようにcartesian座標をとる。各vertexのhomogeneous座標をcartesian座標から、(x, y, z) -> (x, y, z, z)となるように定める。そののち、各vertexのhomogeneous座標を第四成分が1となるように規格化（各成分を第四成分で割る）する。規格化後の座標が(x', y', 1, 1)なら、投影後の座標は(x', y')だ。このように、遠近法に関する計算を楽に行える。だから、homogeneous座標系はグラフィックス分野で多用されるらしい（本当はこの分野に来てまだ３日なので何もわかってない）。